

We shall use the following notation for average slopes in the x and y directions: The first and second partial derivatives of f(x, y) exist for (x, y) in the rectangle I was reading the long road to calculus in section 5.5 and I stumbled upon. Say we want to drive to San Francisco, which.

Then, there exists some value c2(a b) such that f0(c) f(b) f(a) b a Intuitively, the Mean Value Theorem is quite trivial. Let f be a continuous function on a b, which is di erentiable on (a b). Let Δx and A3 1 be positive infinitesimals. 1 Mean Value Theorem The Mean Value Theorem is the following result: Theorem 1.1 (Mean Value Theorem). I will not say that progress in this direction is impossible, but it is true that none of the investigators have achieved anything positive. Question 3.The plan is to prove a corresponding result for average slopes and then use the Mean Value Theorem, which states that the average slope of a function on an interval is equal to the slope at some point in the interval. The first and chief problem of this analysis would be to prove the mean-value theorem f(x+h)-f(x)h \cdot f'(x+\vartheta h) from the assumed axioms.

Did Klein elaborate in this direction in other works of his? Now this is interesting, 'cause here we have a derivative, here we have an. When Klein writes that none of the current investigators have achieved, etc., who is he referring to? There were a number of people working "in this direction" at the time, and it would be interesting to know whose work Klein had in mind: Stolz, Paul du Bois-Raymond (somewhat earlier), Hahn, Hilbert, etc. Remember, what we saw for the average value of a function, we said the average value of a function is going to be equal to 1 over b minus a, notice, 1 over b minus a, you have a b minus a in the denominator here, times the definite integral from a to b, of f of x dx. Therefore, the conclude the Mean Value Theorem, it states that there is a point ‘c’ where the line that is tangential is parallel to the line that passes through (a,f(a)) and (b. definition of a limit by means of the notion value approached has. The value is a slope of line that passes through (a,f(a)) and (b,f(b)). A course dealing with the fundamental theorems of infinitesimal calculus in a. Extreme Value Theorem, which says that any real valued continuous function on a closed. The mean value theorem can be proved using the slope of the line.
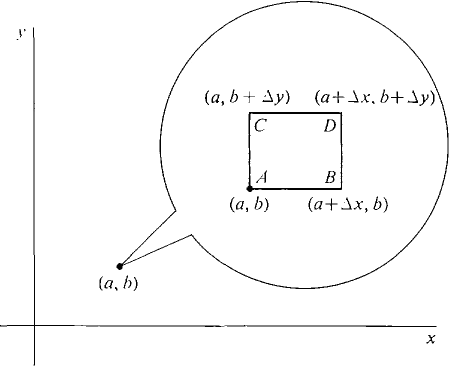
Arithmetic, algebra, analysis) originally published in 1908 in German. The proof of the theorem is given using the Fermats Theorem and the. Calculus texts then go on to use Rolles Theorem to arrive at and prove the Mean. This comment appears on page 219 in the book (Klein, Felix Elementary mathematics from an advanced standpoint. infinitesimals have anything to do with the large scale behavior of the function. I will not say that progress in this direction is impossible, but it is true that none of the investigators have achieved anything positive. Proof: The mean value theorem tells us that. The first and chief problem of this analysis would be to prove the mean-value theorem $$ f(x+h)-f(x)=h \cdot f'(x+\vartheta h) $$ from the assumed axioms. As an example, take the function f : 0, ) 1, 1 defined by f(x) sin(1/x) for x > 0 and f(0) 0. However, not every Darboux function is continuous i.e., the converse of the intermediate value theorem is false. it would be possible to modify the traditional foundations of infinitesimal calculus, so as to include actually infinitely small quantities in a way that would satisfy modern demands as to rigor in other words, to construct a non-Archimedean system. In any interval the mean value theorem tells us that the difference in f between its endpoints is their separation times the derivative of f at some. The intermediate value theorem says that every continuous function is a Darboux function. Namely, one must be able to prove a mean value theorem (MVT) for arbitrary intervals, including infinitesimal ones: In 1908, Felix Klein formulated a criterion of what it would take for a theory of infinitesimals to be successful. This is a reference request prompted by some intriguing comments made by Felix Klein. 17 contains the proof of the following theorem: Iff(x) is continuous in (a, b) and if for a certain value M the roots of the equation f(x) M are everywhere.


 0 kommentar(er)
0 kommentar(er)
